Question 2 (a)

The probability that all 3 people selected are women can be calculated using the multiplication rule, as follows: P(all three selected are women) first is a woman) XP(second is a womanlfirst is a woman) x P(third is a womanlfirst two are women) 321 = —x 0.012 98 7

Question 2 (c)

No, the process does not correctly simulate the random selection of three women from a group of nine people of whom st'. are men and three are women. The random selection of three people among nine IS done without replacement. However, in the simulation with the dice, the three dice rolls in any given trial are independent of one another, indicating a selection process that is done with replacement.

Question 3 (c)

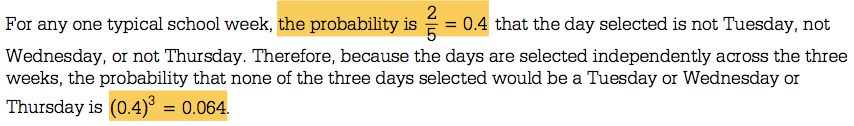
= 0.4 that the day selected is not Tuesday, not For any one typical school week, the probability is Wednesday, or not Thursday. Therefore, because the days are selected independently across the three weeks, the probability that none of the three days selected would be a Tuesday or Wednesday or . 3=0.064. Thursday is (0 4)

Question 4 (a)

The median is less affected by skewness and outliers than the mean. With a variable such as income, a small number of very large incomes could dramatically increase the mean but not the median. Therefore, the median would provide a better estimate of a typical income value.

Question 5

Step 1 : States a correct pair of hypotheses. Let represent the population mean difference in purchase price (woman man) for identically equipped cars of the same model, sold to both men and women by the same dealer, in the county. The hypotheses to be tested are Ho : "diff = O versus Ha : "diff \> Step 2: Identifies a correct test procedure (by name or by formula) and checks appropriate conditions. The appropriate procedure is a paired t-test. The conditions for the paired t-test are: 1. The sample is randomly selected from the population. 2. The population of price differences (woman man) is pprmally distributed, or the sample size is jårge, The first condition is met because the car models and the individuals were randomly selected. The sample size ( n = 8 ) is not large, so we need to investigate whether it is reasonable to assume that the population of price differences is normally distributed. The dotplot of sample price differences reveals a fairly symmetric distribution, so we will consider the second condition to be met. Step 3: Correct mechanics, including the value of the test statistic andp-value (or rejection region). The test statistic is 530.71 The p-value, based on a t-distribution nhth — 1 = 7 degrees of freedom, is 0.008. Step 4: States a correct conclusion in the context of the study, using the result of the statistical test. Because the p-value is very small (for instance, smaller than a = 0.05 ), we reject the null hypothesis. The data provide convincing evidence that, on average, women pay more than men in the county for the same car model.

  • Assumption in 2 sample independence T-test

    • Normality: Assumes that the population distributions are normal. The t-test is quite robust over moderate violations of this assumption. It is especially robust if a two tailed test is used and if the sample sizes are not especially small. Check for normality by creating a histogram.

    • Independent Observations: The observations within each treatment condition must be independent.

    • Equal Variances: Assume that the population distributions have the same variance. This assumption is quite important (If it is violated, it makes the test’s averaging of the 2 variances meaningless).

    • If it is violated, then use a modification of the t-test procedures as needed.

  • Paired Sample T test

    • The matched-pair t-test (or paired t-test or paired samples t-test or dependent t-test) is used when the data from the two groups can be presented in pairs, For example where the same people are being measured in before-and-after comparison or when the group is given two different tests at different times (e.g. pleasantness of two different types of chocolate).

  • Assumptions in paired sample t-test

    • The first assumption in the paired sample t-test is that only the matched pair can be used to perform the paired sample t-test.

    • In the paired sample t-test, normal distributions are assumed.

    • Variance in paired sample t-test: in a paired sample t- test, it is assumed that the variance of two sample is same.

    • The data is measurement data-interval/ratio

    • Independence of observation in paired sample t-test: in a paired sample t-test, observations must be independent of each other.

  • Paired t-test vs two-sample t-test

    A Paired t-test Is Just A I-Sample t-Test Many people are confused about when to use a paired t-test and how it works. I'll let you in on a little secret. The paired t-test and the 1 -sample t-test are actually the same test in disguise\! As we saw above, a I-sample t-test compares one sample mean to a null hypothesis value. A paired t-test simply calculates the difference between paired observations (e.g., before and after) and then performs a 1 -sample t-test on the differences.

    How T-tests Calculate T-Values The 2-sample t-test takes your sample data from two groups and boils it down to the t-value. The process is very similar to the 1 -sample t-test, and you can still use the analogy of the signal-to-noise ratio. Unlike the paired t-test, the 2-sample t-test requi independent groups for each sample.

  • Paired t- test

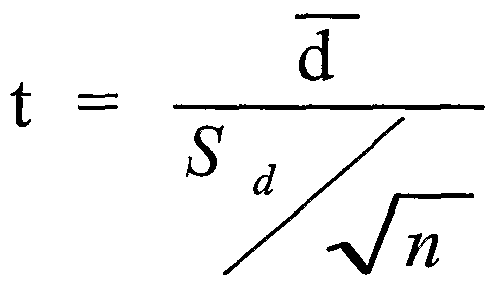
    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image420.png

Question 6 (b)

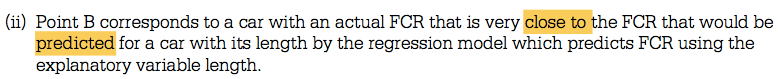
(ii) Point B corresponds to a car with an actual FCR that is very close to the FCR that would be predicted for a car with its length by the regression model which predicts FCR using the explanatory variable length.

Question 6 (c)

Graph Il reveals a moderate association that is positive and linear. In contrast, there is a weak association that is positive and linear in graph Ill. The association between engine size and residual (from predicting FCR based on length) is stronger than the association between wheel base and residual (from predicting FCR based on length).

Question 6 (d)

Engine size is a better choice than wheel base for including with length in a regression model for predicting FCR. The stronger association between engine size and residual (from predicting FCR based on length) indicates that engine size is more useful than wheel base for reducing the variability in FCR values that unexplained (as indicated by residuals) after predicting FCR based on length.

results matching ""

    No results matching ""